Markham Saturday 14:00 Java Homework 21.01.30.

Question 1: (If you have finished this question, please try Question 2)
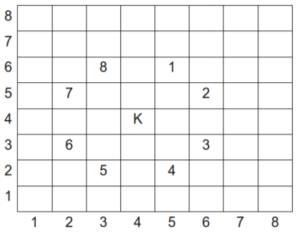
Below is an 8 × 8 chessboard on which we will designate square locations using the ordered pairs as indicated. For example, notice that piece A is at position (2, 2) and piece B is at position (4, 3).

A knight is a special game piece that can leap over other pieces, moving in the “L” pattern. Specifically, in the diagram below, K represents the knight’s starting position and the numbers 1 through 8 represent possible places the knight may move to.

Your program will read the starting location of the knight and output the smallest number of jumps or moves needed to arrive at a location specified in the second input.

Input Specification
Your program will read four integers, where each integer is in the range 1…8. The first two integers represent the starting position of the knight. The second two integers represent the final position of the knight.

Output Specification
Your program should output the minimum (non-negative integer) number of moves required to move the knight from the starting position to the final position. Note that the knight is not allowed to move off the board during the sequence of moves.

Sample Input 1
2 1
3 3

Output for Sample Input 1
1

Sample Input 2
4 2
7 5

Output for Sample Input 2
2

Question 2:
You have to determine if it is possible to escape from a room. The room is an M-by-N grid with each position (cell) containing a positive integer. The rows are numbered 1, 2, . . . , M and the columns are numbered 1, 2, . . . , N. We use (r, c) to refer to the cell in row r and column c.

You start in the top-left corner at (1, 1) and exit from the bottom-right corner at (M, N). If you are in a cell containing the value x, then you can jump to any cell (a, b) satisfying a × b = x. For example, if you are in a cell containing a 6, you can jump to cell (2, 3).

Note that from a cell containing a 6, there are up to four cells you can jump to: (2, 3), (3, 2), (1, 6), or (6, 1). If the room is a 5-by-6 grid, there isn’t a row 6 so only the first three jumps would be possible.

Input Specification
The first line of the input will be an integer M (1 ≤ M ≤ 1000). The second line of the input will be an integer N (1 ≤ N ≤ 1000). The remaining input gives the positive integers in the cells of the room with M rows and N columns. It consists of M lines where each line contains N positive integers, each less than or equal to 1 000 000, separated by single spaces.

Output Specification
Output yes if it is possible to escape from the room. Otherwise, output no.

Sample Input
3
4
3 10 8 14
1 11 12 12
6 2 3 9

Output for Sample Input
yes

Explanation of Output for Sample Input
Starting in the cell at (1, 1) which contains a 3, one possibility is to jump to the cell at (1, 3).
This cell contains an 8 so from it, you could jump to the cell at (2, 4). This brings you to a cell
containing 12 from which you can jump to the exit at (3, 4). Note that another way to escape is to
jump from the starting cell to the cell at (3, 1) to the cell at (2, 3) to the exit.

Notes
1. The online grader begins by testing submissions using the sample input. All other tests are skipped if the sample test is not passed. If you are only attempting the first three subtasks (the first 7 marks), then you might want to handle the specific values of the sample input as a special case.

2. For the final subtask (worth 2 marks), if you are using Java, then Scanner will probably take too long to read in the large amount of data. A much faster alternative is BufferedReader.